Determining Roll and Pitch of a Body from the Gravity Vector

Problem: Determine Pitch and Roll from the gravity vector measured via 3-orthogonal accelerometers measured by an Inertial Measurement Unit.

First constructing the coordinate transformation matrix for Euler transformations about the y-axis (pitch) and then about the x-axis (roll). The conventional first rotation about the inertial z-axis (yaw) is ignored since changes in yaw does not effect the accelerations measured by the body axis accelerations.

Refer to Figure 1 below where theta, single prime and red represent the first rotation (pitch) and phi, double prime and blue represent the second rotation (roll).

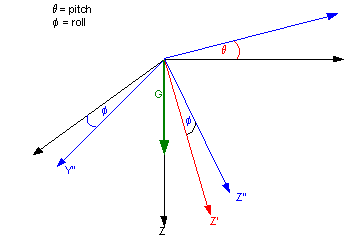
Figure 1
Euler Rotations in Pitch and Yaw

The coordinate transformation from the resulting rotated body frame to the inertial reference frame, which is defined as north-east-down (NED) frame with the z-axis collinear with the gravity vector:

T = [ M1 * M2 ] T’’

Where:

| cos(theta) 0 sin(theta) |

M1 = | 0 1 0 |

|-sin(theta) 0 cos(theta) |

| 1 0 0 |

M2 = | 0 cos(phi) -sin(phi) |

| 0 sin(phi) cos(phi) |

Multiplying the M1 and M2 and using the following notation for brevity:

c1 = cos(theta)

s1 = sin(theta)

c2 = cos(phi)

s2 = sin(phi)

gives:

| c1 s2s1 c2s1 |

M1 * M2 = | 0 c2 s2 |

| -s1 s2c1 c2c1 |

For our given situation plugging in the known values we have:

| 0 | | c1 s2s1 c2s1 | | ax |

| 0 | = | 0 c2 s2 | * | ay |

| G | | -s1 s2c1 c2c1 | | az |

Where G is the gravity vector and ax,ay, and az are the measured accelerations in the body axis.

From this the roll is readily found as:

c2*ay + s2*az = 0

roll = arctan(ay/az) Eqn 1

To find pitch is a little more difficult. Although it is possible to solve the above equations explicitly for theta (pitch), the last remaining unknown, as a function of (phi,ax,ay,az) a cleaner solution is found by examining the geometry. Pitch is defined as the angle between the vertical gravity vector and the y-z plane. This can be found by dividing the measured magnitude of gravity vector in the y-z plane by the gravity vector.

Tan(q) = sqrt(ay^2 + az^2)/ g

But since g = sqrt(ax^2 + ay^2 +az^2) we have pitch as:

Pitch = arctan{sqrt(ay^2+az^2)/(sqrt(ax^2+ay^2+az^2) } Eqn 2